人教版高中數學選修3二項式定理教學設計(內容全面)
Word格式/內容可修改





例2.(1)求(1+2x)^7的展開式的第4項的系數;(2)求(2√x-1/√x)^6的展開式中x^2的系數.解:(1+2x)^7的展開式的第4項是T_(3+1)=C_7^3×1^(7-3) ×〖(2x)〗^3=C_7^3×2^3 ×x^3=35×8 ×x^3=280 x^3因此,展開式第4項的系數是280.(2)(2√x-1/√x)^6 的展開式的通項是C_6^k 〖(2x^(1/2))〗^(6-k) 〖(x^(-1/2))〗^k=〖C_6^k 2〗^(6-k) x^((6-k)/2-k/2)=〖C_6^k 2〗^(6-k) x^(3-k)根據題意,得3-k=2,k=1 ,因此,x^2 的系數是〖(-1)×2〗^5×C_6^1=-192.二項式系數與項的系數的求解策略 (1)二項式系數都是組合數C_n^k(k∈{0,1,2,…,n}),它與二項展開式中某一項的系數不一定相等,要注意區分“二項式系數”與二項展開式中“項的系數”這兩個概念.(2)第k+1項的系數是此項字母前的數連同符號,而此項的二項式系數為C_n^k.例如,在(1+2x)7的展開式中,第4項是T4=C_7^317-3(2x)3,其二項式系數是C_7^3=35,而第4項的系數是C_7^323=280.跟蹤訓練2. (1)求二項式 2√x-1/x 6的展開式中第6項的二項式系數和第6項的系數;(2)求 x-1/x 9的展開式中x3的系數.解:(1)由已知得二項展開式的通項為Tk+1=C_6^k(2√x)6-k· -1/x k=26-kC_6^k·(-1)k·x^(3"-" 3k/2),∴T6=-12x^("-" 9/2).∴第6項的二項式系數為C_6^5=6,第6項的系數為C_6^5·(-1)5·2=-12.(2)設展開式中的第k+1項為含x3的項,則Tk+1=C_9^kx9-k -1/x k=(-1)kC_9^kx9-2k,令9-2k=3,得k=3,即展開式中第4項含x3,其系數為(-1)3·C_9^3=-84.
轉載請注明出處!本文地址:
http://www.cwhmytx.cn/wd/20231101141946786.html- 軟件:Office 2016及以上版本
- 格式:docx
- 文件大小:490.51KB
- 頁數:10
- 編號:20231101141946786
- 售價:5 金幣 / 會員免費
- 上傳時間:2023-11-01
- 上傳者:梁小A-PPT
- 肖像權:人物畫像及字體僅供參考
-
人教版高中數學選修3二項式定理教學設計(內容全面)
教育教學模板 | 頁數:10 -
人教版高中數學選修3二項式系數的性質教學設計(內容詳細)
教育教學模板 | 頁數:8 -
人教版高中數學選修3成對數據的相關關系教學設計(內容型)
教育教學模板 | 頁數:14 -
人教版高中數學選修3分類變量與列聯表教學設計(內容完整)
教育教學模板 | 頁數:19 -
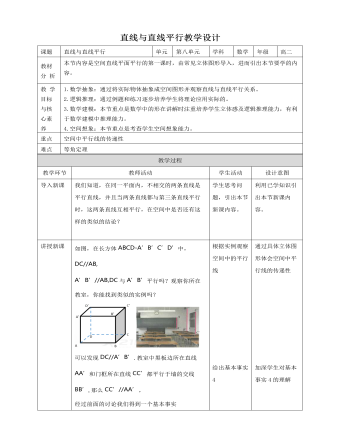
人教A版高中數學必修二直線與直線平行教學設計(內容全面)
教育教學模板 | 頁數:6 -
人教A版高中數學必修一函數的概念教學設計(2)(內容全面)
教育教學模板 | 頁數:9 -
人教A版高中數學必修一函數模型的應用教學設計(2)(內容全面)
教育教學模板 | 頁數:7